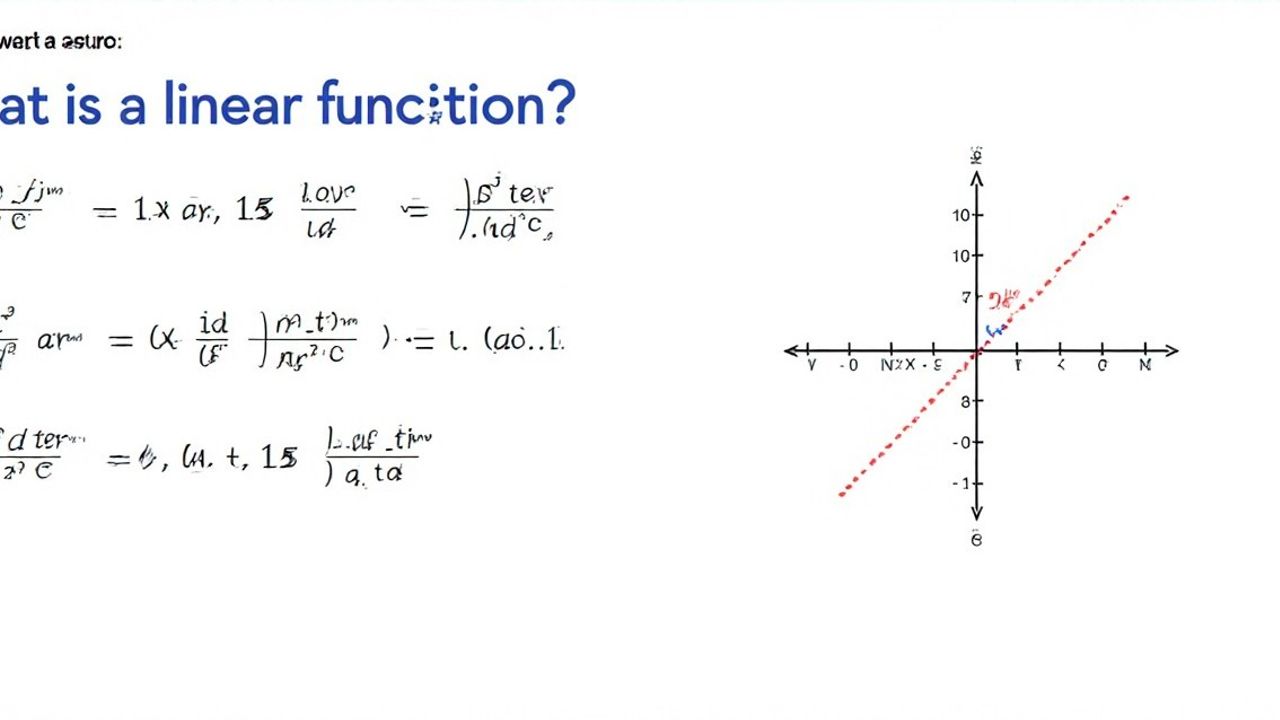
Bu, fonksiyonun bağımsız değişkenindeki (x) her bir birimlik artışta, bağımlı değişkenin (y) de sabit bir miktar artması veya azalması anlamına gelir. Bu sabit miktar, çizginin eğimi olarak adlandırılır.
10. Sınıf Seviyesinde Doğrusal Fonksiyonlar
10. sınıfta doğrusal fonksiyon kavramı daha matematiksel olarak ele alınır. Bir doğrusal fonksiyon, f(x) = ax + b şeklinde ifade edilir, burada 'a' ve 'b' sabit sayılardır ve 'a' fonksiyonun eğimini, 'b' ise y-kesişimini (yani, grafiğin y eksenini kestiği noktayı) temsil eder. 'a' değeri sıfırdan farklıysa, fonksiyon doğrusaldır. 'a' değeri sıfır ise, fonksiyon sabit bir fonksiyondur ve yatay bir çizgiyi temsil eder.
Doğrusal Referans Fonksiyon Nedir?
Doğrusal referans fonksiyon terimi genellikle doğrusal fonksiyonun özel bir durumunu veya uygulamasını belirtmek için kullanılmaz. Doğrusal fonksiyonun kendisi, diğer fonksiyonları veya verileri referans almak veya modellemek için kullanılabilir. Örneğin, lineer regresyon analizinde, verilerin dağılımına en iyi uyan doğrusal fonksiyon bulunarak, veriler arasında bir ilişki kurulabilir ve bu fonksiyon bir referans fonksiyonu olarak kullanılabilir.
Doğrusal Fonksiyon Örneği
Pratik Bir Örnek
Örneğin, f(x) = 2x + 3 fonksiyonunu ele alalım. Bu bir doğrusal fonksiyondur çünkü ax + b formunda olup, a=2 ve b=3'tür. Eğer x=1 ise, f(1) = 2(1) + 3 = 5 olur. x=2 ise, f(2) = 2(2) + 3 = 7 olur. Görüldüğü gibi, x'teki her bir birimlik artışta, y'de 2 birimlik bir artış vardır. Bu sabit artış, fonksiyonun eğimini (2) gösterir.
Doğrusal Fonksiyon Formülü Nedir?
Doğrusal fonksiyonun genel formülü f(x) = ax + b şeklindedir. Burada:
f(x): Fonksiyonun değeri (bağımlı değişken)
x: Bağımsız değişken
a: Eğimi (x'teki her bir birimlik değişikliğe karşılık gelen y'deki değişim)
b: Y-kesişimi (grafiğin y eksenini kestiği nokta)
Doğrusal Olmayan Fonksiyon Nedir?
Doğrusal olmayan fonksiyonlar, grafiği düz bir çizgi olmayan fonksiyonlardır. Bunların eğimleri sabit değildir ve f(x) = ax + b formunda ifade edilemezler. Örnek olarak, f(x) = x², f(x) = sin(x) veya f(x) = 2x gibi fonksiyonlar verilebilir. Bu fonksiyonların grafikleri eğrilerdir.
Doğrusal Fonksiyon Tanımı - Kısaca
Kısaca, doğrusal fonksiyon, grafiği düz bir çizgi olan ve f(x) = ax + b formunda ifade edilebilen bir fonksiyondur. Tanımlı olduğu aralıkta, bağımsız değişkendeki her birimlik değişim için bağımlı değişkendeki değişim sabittir.
Doğrusal Fonksiyonun Tanımlı Olduğu Aralık
Bir doğrusal fonksiyon, gerçek sayılar kümesinin tümünde tanımlıdır. Yani, x'in alabileceği değerler sınırsızdır. Bu, fonksiyonun grafiğinin tüm x değerleri için devam ettiğini gösterir.